Tutorial 3: SciPy¶
This sections shows several examples how to use module SciPy. See module homepage for more tutorials, reference manual.
Integration¶
import scipy.integrate as sc import numpy as np # 1-D sc.quad(lambda x :np.exp(-x**2), -np.inf, np.inf)[0] 1.77245385091 # 2-D sc.dblquad(lambda x, y: x*y, 0, 2, lambda x: 0, lambda x: 2)[0] 4.0
Interpolation¶
import scipy.interpolate as sc import matplotlib.pyplot as plt # 1-D x = np.linspace(0, 10, 11) y = np.sin(x) x2 = np.linspace(0, 10, 100) y2 = sc.interp1d(x, y) plt.figure() plt.plot(x, y, 'o') plt.plot(x2, y2(x2)) plt.show()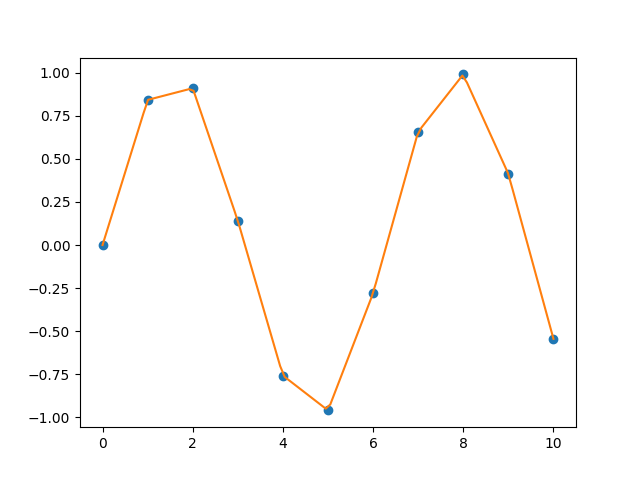
Fourier transform¶
import scipy.fftpack as sc # 2 waves N = 600 T = 1.0 / 800.0 x = np.linspace(0.0, N*T, N) y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x) xf = np.linspace(0.0, 1.0/(2.0*T), N//2) yf = sc.fft(y) plt.figure() plt.plot(xf, 2.0/N * np.abs(yf[0:N//2])) plt.show()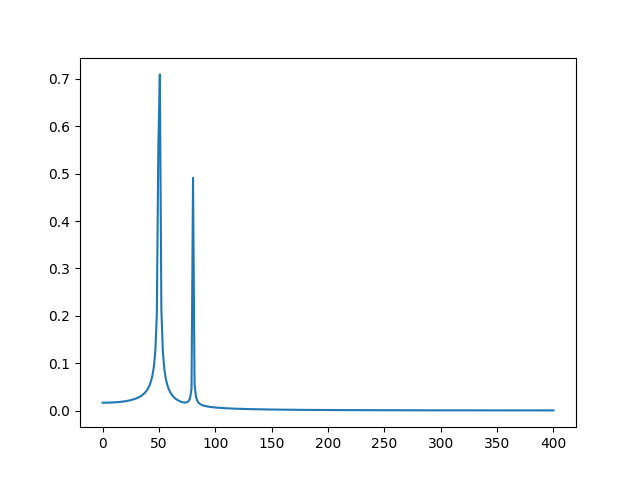
Signal processing¶
import scipy.signal as sc # FIR filters - low pass, band stop b1 = sc.firwin(40, 0.5) b2 = sc.firwin(41, [0.3, 0.8]) w1, h1 = sc.freqz(b1) w2, h2 = sc.freqz(b2) plt.figure() plt.title('Digital filter frequency response') plt.plot(w1, 20*np.log10(np.abs(h1)), 'b', label='low pass') plt.plot(w2, 20*np.log10(np.abs(h2)), 'r', label='band stop') plt.ylabel('Amplitude Response (dB)') plt.xlabel('Frequency (rad/sample)') plt.legend() plt.show()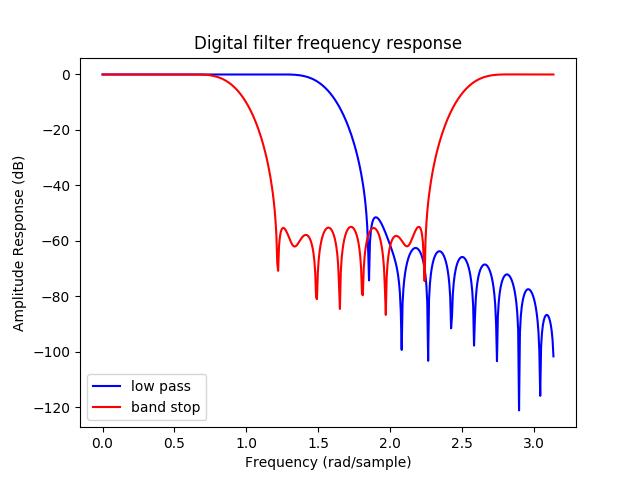
Linear algebra¶
import scipy.linalg as sc # set of linear equations A = np.array([[1, 2], [3, 4]]) b = np.array([[5], [6]]) # via inverse matrix sc.inv(A).dot(b) [[-4. ] [ 4.5]] # via solver sc.solve(A, b) [[-4. ] [ 4.5]]
Statistics¶
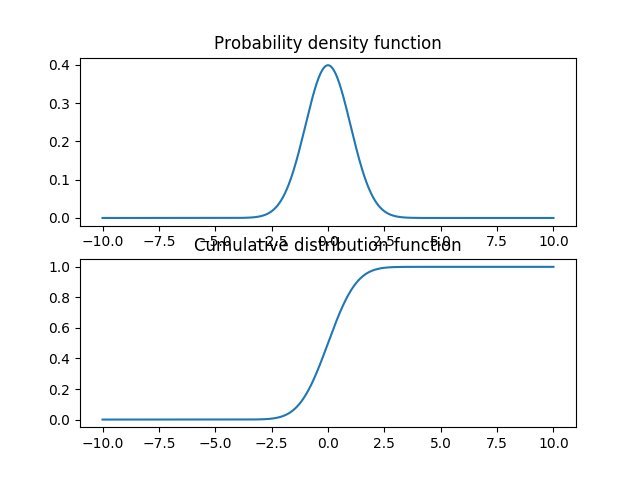
import scipy.stats as sc # statistical parameters x = sc.norm(size=100) mean, std, var = x.mean(), x.std(), x.var() (0.017051340606627, 0.97538562220022185, 0.95137711199491382) # PDF, CDF x = np.linspace(-10, 10, 1000) y1 = sc.norm.pdf(x) y2 = sc.norm.cdf(x) plt.figure() plt.subplot(211) plt.plot(x, y1) plt.title('Probability density function') plt.subplot(212) plt.plot(x, y2) plt.title('Cumulative distribution function') plt.show()